Our member, Prof. Joaquin Torres, has recently published a very interesting paper in the top journal Phys. Rev. Lett. In collaboration with Ana P. Millán (Vrije Universiteit Amsterdam) and Prof. Ginestra Bianconi (Queen Mary University of London), Prof. Torres has studied the phenomenon of synchronization.
Synchronization is a collective phenomenon that pervades the natural system from neurons to fireflies. In a network, synchronization of the dynamical variables associated with the nodes occurs when nodes are coupled to their neighbours as captured by the Kuramoto model. However, many complex systems include also higher-order interactions among more than two nodes and sustain dynamical signals that might be related to higher-order simplices such as links and triangles. These dynamical topological signals include for instance fluxes which are dynamical variables associated with links.
In the present work, we combine synchronization theory with topology and we propose the higher-order Kuramoto model that provides the main synchronization route for topological signals. The researchers show that the dynamics defined on links can be projected to a dynamics defined on nodes and triangles that undergo a synchronization transition.
Interestingly, when the model includes an adaptive coupling of the two projected dynamics, the transition becomes explosive, i.e. synchronization emerges abruptly.
This model can be applied to study synchronization of topological signals in the brain and in biological transport networks as it proposes a new set of topological transformations that can reveal collective synchronization phenomena that could go unnoticed otherwise.

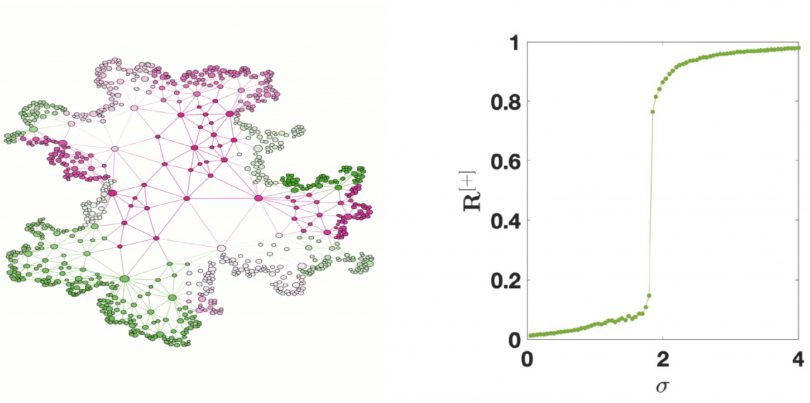
An example of simplicial complex capturing higher-order interactions and sustaining topological signals (on the left) and evidence for explosive synchronization in higher-order Kuramoto model (on the right).
Reference:
Ana P. Millán, Joaquín J. Torres, and Ginestra Bianconi. Explosive Higher-Order Kuramoto Dynamics on Simplicial Complexes. Phys. Rev. Lett. 124, 218301 (2020).
https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.124.218301